

大家好,经过前三篇数据结构文章的学习。对于数组和链表以及线性结构的应用——栈有了初步的认识,这篇文章趁热打铁学习线性结构的另外一种应用——队列
队列(Queue)是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以只有最早进入队列的元素才能最先从队列中删除,故队列又称为先进先出(FIFO—first in first out)线性表。综上,只要能满足“先进先出”条件的线性表,称之为队列。
概念看完了我们接着来。首先看队列有几种形式,第一种静态队列和第二种动态队列。类似于栈的两种形式,静态队列是用数组实现的,而动态队列的核心是链表。
我们知道队列有几个专有名词:前端(front)、后端(rear)、队尾、队头、入队。那如何创建一个队列呢?
类似排队买票,有队头队尾买完票走掉,和新来的人排在队伍的后方。在这里,我用一个数组来模拟人们排队买票的情景,首先指定一个元素指向队伍最前面的那个人,自然就有另一个元素代表队尾。当队伍后方有人来排队的时候,需要将队尾元素指向这个人,有人离开队伍时,应该将队头变量指向离开的人的后一个人。
在前面的三篇笔记中,无论是链表还是栈都预留了一个“无意义”的结点,来充当头结点或尾结点。这里我们也保留这个优良传统,我们定义,队尾变量永远指向最后一个有效元素的后一个元素。
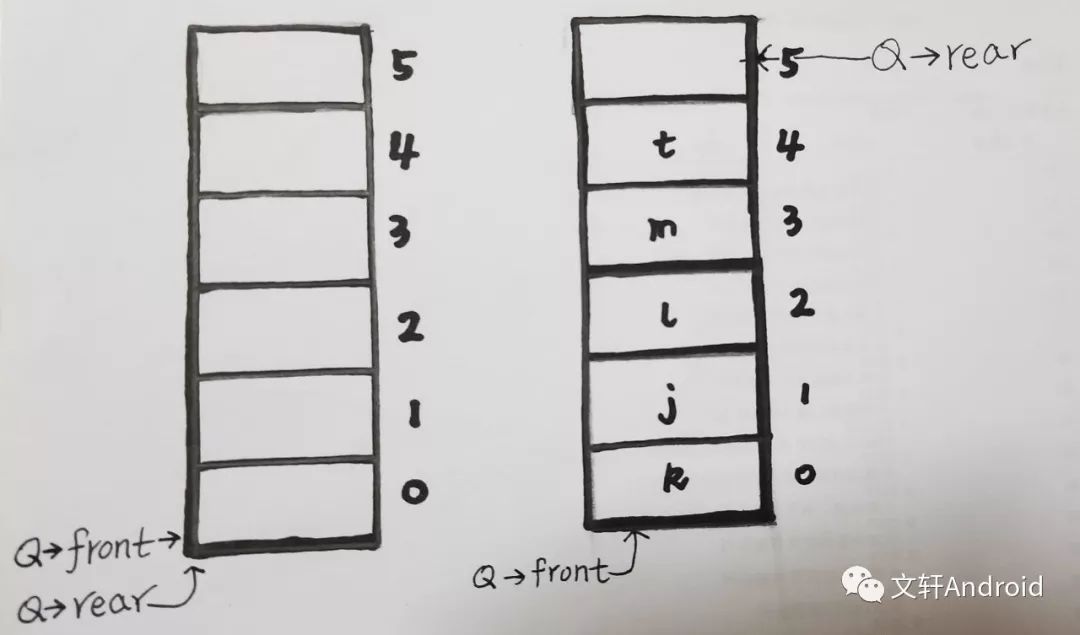
现在我们有一个长度为6的数组,它的下标自然为0、1、2、3、4、5
front保存了队头的下标值,rear保存了队尾最后一个有效元素的下一个元素的下标值。
第一种情况,front为0,rear为5指向数组的最后一个元素,当再进行入队操作时,首先把值存入当前r保存的下标值对应的元素中,然后把rear加一,但是,如果再加一,数组就会越界。然而此时又不宜如栈那样,进行存储再分配扩大数组空间,因为队列的实际可用空间并未占满。
第二种情况,f指向队头,r指向最后一个有效元素的下一个元素,每次入队r都会加一,假如现在r增加到了4,想进行出队操作(此时队列中有4个元素),需要将f增加,f增加到了2,此时相当于只剩2个元素,删除了前两个元素,这样就会造成我们被删除的位置永远无法再被利用,就会造成空间的浪费。所以,一般的数组就达不到要求了,所以静态队列需要用循环队列。
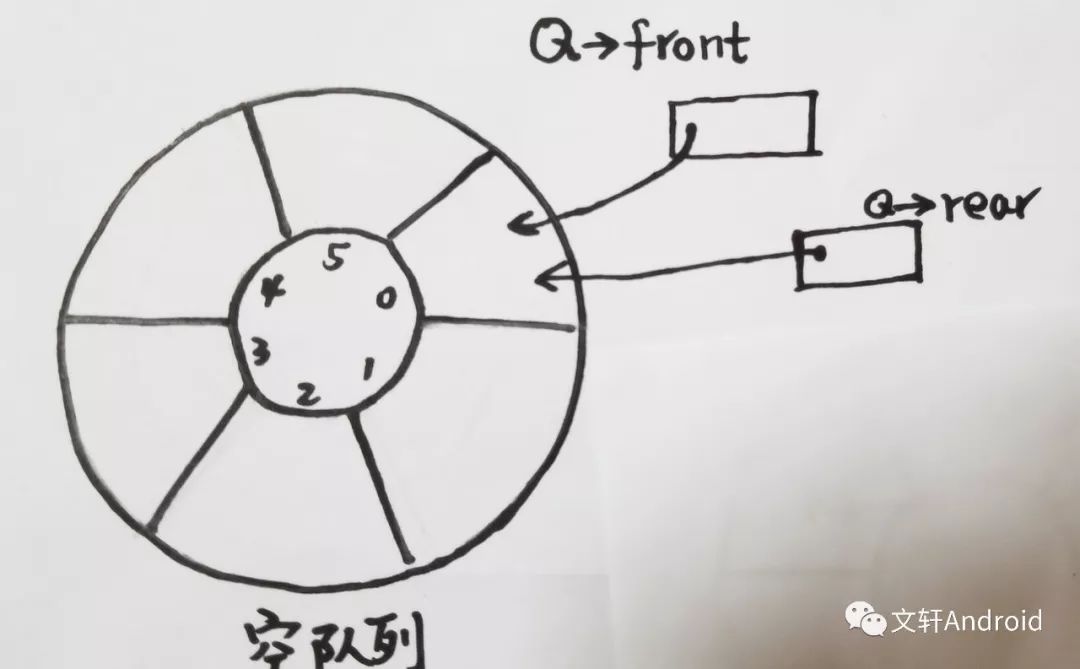
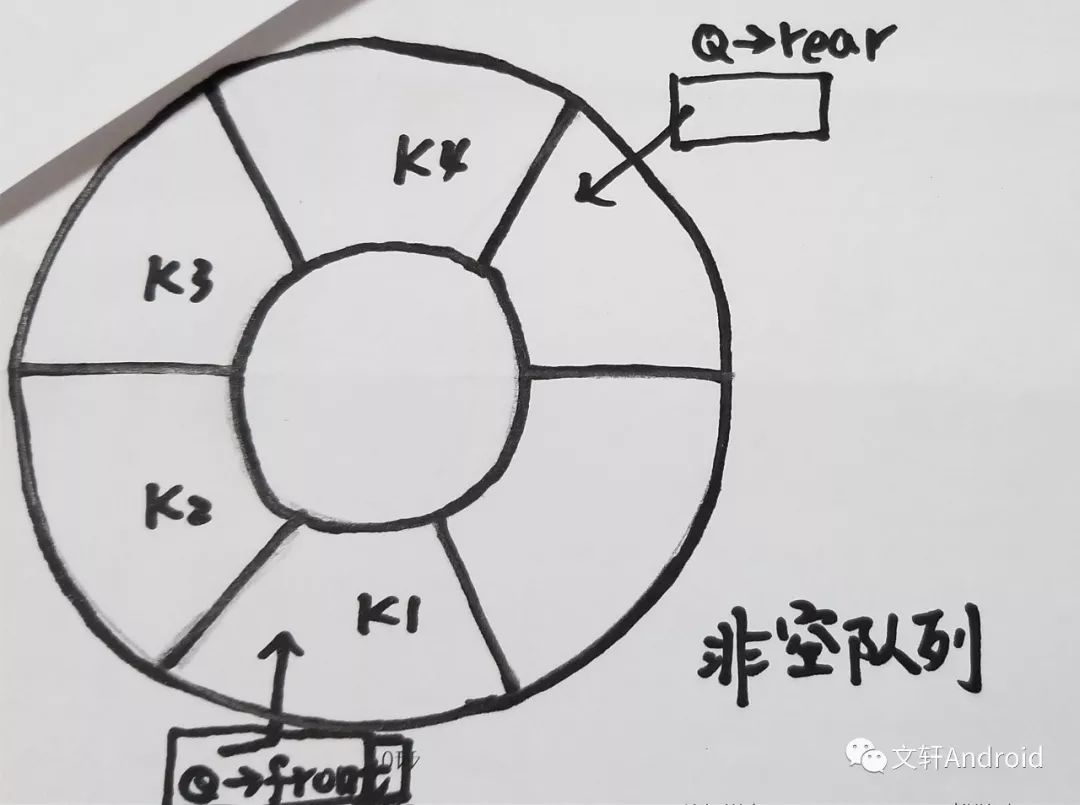
在正式学习循环队列之前,先要弄清楚几个问题:
根据前面的描述,创建循环队列需要2个参数来确定front,rear。
1.两个参数代表的含义始终是一样的吗?
在这里两个参数在不同的场合下有不同的含义:
(1)初始化队列时:front和rear都是0
(2)队列非空时:front代表队列的第一个元素,rear则代表的是最后一个有效元素的下一个元素
(3)队列为空时,front和rear的值相等,但不一定是0
2.如何判断队列为空?
这个问题简单,front的值和rear相等即可
3.如何判断队列已满
再循环队列中,如果每个结点都放上元素,front和rear就会重合,这样无法判断队列的当前状态了,所以一个长度为N的队列存放N-1个元素,对应代码(rear + 1) % len == f 判断这个表达式的布尔值即可。
老规矩,先定义队列的基本结构
typedef struct Queue {
int * pBase;
int front;
int rear;
}QUEUE;类似于上文的创建空队列的方法,将front和rear的值都等于0,分配的空间赋给pBase
// 初始化队列
void init(QUEUE * pQ) {
pQ->pBase = (int *)malloc(sizeof(int) * 6); // 分配空间
pQ->front = 0;
pQ->rear = 0;
}定义一些循环队列基本的函数
void init(QUEUE *); // 初始化队列
bool en(QUEUE *, int val); // 入队
bool full(QUEUE * );
void trasevel(QUEUE *); // 遍历队列
bool out(QUEUE *, int * ); // 出队
bool empty(QUEUE * ); // 是否为空其中,入队的写法要注意先判断当前队列是否已满。队列不是满的状态下,
把值放在rear下标对应的元素里。而后,将rear的值通过rear+1和长度取余的方式,让rear往后走一个
// 判断队列是否为满
bool full(QUEUE * pQ) {
if( (pQ->rear + 1) % 6 == pQ->front) {
return true;
}else {
return false;
}
}
// 入队
bool en(QUEUE * pQ, int val) {
if(full(pQ)) {
// 队列满了,不能入队
return false;
}else {
pQ->pBase[pQ->rear] = val; //把值放在r下标对应的元素里
pQ->rear = (pQ->rear + 1) % 6; //r往后走一个
return true;
}
}#include <stdio.h>
#include <malloc.h>
typedef struct Queue {
int * pBase;
int front;
int rear;
}QUEUE;
void init(QUEUE *); // 初始化队列
bool en(QUEUE *, int val); // 入队
bool full(QUEUE * );
void trasevel(QUEUE *); // 遍历队列
bool out(QUEUE *, int * ); // 出队
bool empty(QUEUE * ); // 是否为空
int main() {
int val;
QUEUE Q;
init(&Q);
en(&Q, 1);
en(&Q, 2);
en(&Q, 3);
en(&Q, 4);
en(&Q, 5);
en(&Q, 6);
trasevel(&Q);
if(out(&Q, &val)) {
trasevel(&Q);
}else {
printf("出队失败n");
}
return 0;
}
// 初始化队列
void init(QUEUE * pQ) {
pQ->pBase = (int *)malloc(sizeof(int) * 6); // 分配空间
pQ->front = 0;
pQ->rear = 0;
}
// 判断队列是否为满
bool full(QUEUE * pQ) {
if( (pQ->rear + 1) % 6 == pQ->front) {
return true;
}else {
return false;
}
}
// 入队
bool en(QUEUE * pQ, int val) {
if(full(pQ)) {
// 队列满了,不能入队
return false;
}else {
pQ->pBase[pQ->rear] = val; //把值放在r下标对应的元素里
pQ->rear = (pQ->rear + 1) % 6; //r往后走一个
return true;
}
}
// 遍历队列
void trasevel(QUEUE * pQ) {
int i = pQ->front; // i存储了f的值
while (i != pQ->rear) {
printf("%d ",pQ->pBase[i]);
i = (i + 1)%6;
}
printf("n");
}
// 是否为空
bool empty(QUEUE * pQ) {
if(pQ->front == pQ->rear) {
return true;
}else {
return false;
}
}
// 出队
bool out(QUEUE * pQ, int * pVal ) {
if(empty(pQ)) {
return false;
}else {
* pVal = pQ->pBase[pQ->front];
pQ->front = (pQ->front + 1)%6; // 变更F的值
return true;
}
}原文始发于微信公众号(代码墙):数据结构学习笔记(四)队列
